Voor de broodnodige variatie! Dat was de slogan van een televisiereclame in de jaren 70. Geen idee over welk product het ging, maar de slogan bleef hangen. Variatie is brood nodig, in je voeding, in de dingen die je doet, de mensen die je ziet en spreekt, of je hard loopt of even stil valt. Altijd hetzelfde eten maakt ziek, altijd hetzelfde doen stompt af, altijd dezelfde mensen zien en spreken gaat vervelen (behalve die ene dan), altijd even hard lopen houd je niet vol. Er moet variatie zijn om ons gezond, vrolijk, alert, hulpvaardig, aimabel, in conditie en gezellig te houden. Variatie is ook nodig in statistiek; de maat die dan gebruikt wordt heet variantie. Zonder variantie houden veel berekeningen ineens op, domweg omdat bij veel berekeningen door de variantie gedeeld wordt en delen door Ø (nul) niet kan. Variatie in het dagelijks leven houdt ons gezond, variantie in de statistiek zorgt ervoor dat we kunnen rekenen.
Ons hele leven bestaat uit variatie: de meesten van ons wijken regelmatig af van de regels; we eten gevarieerd – de een meer dan de ander, wat op zich weer zorgt voor variatie in de variatie -; niemand houdt het vol om een weg van 100 km lang constant 100 km/h te rijden – dat kan alleen een cruise control – ; de ene dag voelen we ons gelukkiger dan de andere dag. We zijn steeds maar in beweging, en zorgen daarmee voor variatie.
Als de spreiding groot is, zeg je vooral over veel mensen niets
Variatie kan ook een veroorzaker van wanorde zijn. Neem het verkeer als voorbeeld. In der tijd werd de maximum snelheid beperkt tot 100 km/h. Later werd die maximum snelheid weer verhoogd, maar de vraag was hoe hoog de nieuwe maximum snelheid moest zijn. Een argument hierbij was, dat bij een lagere snelheid minder ongelukken gebeuren dan bij een hogere snelheid, zeg 120 km/h. De gedachtegang had moeten zijn: als de maximum snelheid 120 km/h is, komt er meer variatie in snelheid op de weg en die variatie leidt tot meer ongelukken en files, niet de gemiddelde of maximum snelheid. Denk maar aan een snelweg waar iedereen 200 rijdt. Geen ongelukken. Pas als variatie optreedt – klapband of plotseling remmen, om er twee te noemen – ontstaat een gevaarlijke situatie. Het leidt tot beweging (uitwijken) en stilstand (botsing) en daarmee file (wanorde). Niet de hoge gemiddelde snelheid is het probleem, maar de variatie in snelheid, zoals ook blijkt uit een factsheet van Stichting Wetenschappelijk onderzoek naar Verkeersveiligheid waar werd gesteld dat “het aantal doden …… op auto(snel)wegen ongeveer een factor vier lager lag dan op wegen met een snelheidslimiet van 80 km/uur” (SWOV, 2013, p 5)
 Wat geeft ons meer informatie: de uitspraak ‘gemiddeld scoren Nederlanders 6,83 op levensgeluk’ of, afgezien van de vraag wat levensgeluk is, het plaatje hiernaast waar het gemiddelde ook 6,83 is? In het plaatje zien we dat er best veel mensen ongelukkig zijn en niet zo heel veel bijzonder gelukkig. Als ik erbij vermeld, dat levensgeluk is gemeten op een schaal van 1 tot 20, wordt beeld weer heel anders. In dat geval zijn we er beroerd aan toe. We zien dus hoe belangrijk inzicht in de variatie is.
Wat geeft ons meer informatie: de uitspraak ‘gemiddeld scoren Nederlanders 6,83 op levensgeluk’ of, afgezien van de vraag wat levensgeluk is, het plaatje hiernaast waar het gemiddelde ook 6,83 is? In het plaatje zien we dat er best veel mensen ongelukkig zijn en niet zo heel veel bijzonder gelukkig. Als ik erbij vermeld, dat levensgeluk is gemeten op een schaal van 1 tot 20, wordt beeld weer heel anders. In dat geval zijn we er beroerd aan toe. We zien dus hoe belangrijk inzicht in de variatie is.
Mijn punt is hier niet hoe gelukkig we nou eigenlijk zijn, maar wat de informatie die we krijgen eigenlijk zegt over de werkelijkheid.
Mensen zijn gek op versimpeling. Het geeft ons schijnbaar grip op de werkelijkheid. Versimpeling heeft ook heel veel opgeleverd, waaronder de wetenschappelijke vooruitgang. Helaas wordt er vaak te veel en onjuist versimpeld, de zogenaamde oversimplificatie, waardoor er een vals beeld ontstaat dat vervolgens zijn eigen leven gaat leiden.
Populaire versimpelingen zijn het gemiddelde en de modus (modaal, weet u wel?). Van de statistieken halen vooral zij de pers; de mediaan komt gek genoeg bijna nooit in het nieuws. In de media wordt uitgelicht hoe Nederland gemiddeld scoort op geluk, rijkdom, uren werk per week, participatie en noem maar op; we hebben een modaal inkomen, er bestaan modale werknemers. Wat zeggen de modus, de mediaan en het gemiddelde nou eigenlijk?
 Elk afzonderlijk geeft maar een beetje informatie. Als je de modus kent, weet je alleen maar welke waarde het meest voorkomt, als je de mediaan kent, weet je alleen maar boven welke waarde 50% van de waarnemingen zit en als je het gemiddelde kent, weet je door het gemiddelde met het aantal waarnemingen te vermenigvuldigen, de som van alle scores. Als je ze alle drie kent, weet je iets over de vorm van de verdeling:
Elk afzonderlijk geeft maar een beetje informatie. Als je de modus kent, weet je alleen maar welke waarde het meest voorkomt, als je de mediaan kent, weet je alleen maar boven welke waarde 50% van de waarnemingen zit en als je het gemiddelde kent, weet je door het gemiddelde met het aantal waarnemingen te vermenigvuldigen, de som van alle scores. Als je ze alle drie kent, weet je iets over de vorm van de verdeling:
gemiddelde < mediaan < modus <=> scheef naar links
modus < mediaan < gemiddelde <=> scheef naar rechts
gemiddelde = mediaan = modus <=> symmetrisch
In het bovenstaande voorbeeld is de verdeling scheef naar links; in het plaatje hier rechts, is de verdeling scheef naar rechts. De plaatjes hieronder zijn de verdelingen allebei symmetrisch. In de voorbeelden hieronder zijn modus, mediaan en gemiddelde aan elkaar gelijk en in dit voorbeeld 5,5.
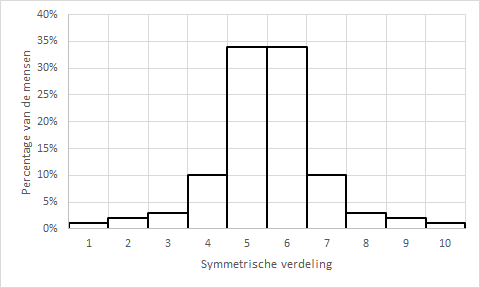 In een ander onderzoek, blijkt Nederland gemiddeld een 5,5 te scoren op iets[1]. Hoe ziet de verdeling eruit? Dat kunnen we zo niet zeggen natuurlijk. Maar als we weten dat ook de mediaan en de modus 5,5 zijn, dan weten we dus dat de verdeling symmetrisch is.
In een ander onderzoek, blijkt Nederland gemiddeld een 5,5 te scoren op iets[1]. Hoe ziet de verdeling eruit? Dat kunnen we zo niet zeggen natuurlijk. Maar als we weten dat ook de mediaan en de modus 5,5 zijn, dan weten we dus dat de verdeling symmetrisch is.
En hoe zit het dan met de variantie, de spreiding?
Daar weten we dan nog niets van. De variantie in een symmetrische verdeling kan klein zijn, zoals hiernaast waar de meeste scoren rond het midden zitten, of groot waar de scores wijd verspreid zijn. Als de spreiding klein is, zegt een gemiddelde meer over het geheel dan als de spreiding groot is. Immers: het gemiddelde zegt dan iets dat bij benadering voor een heleboel mensen (waarnemingen) opgaat. Als de spreiding groot is, zeg je alleen met het gemiddelde (of modus of mediaan) vooral over heel veel mensen (waarnemingen) niets. Het modale inkomen zegt mij dan ook weinig: ik ben benieuwd naar de spreiding van inkomens, gewoon een plaatje.
 Spreiding kan een dramatische vorm aannemen. In het plaatje hiernaast staat een zogenaamde uniforme verdeling: elke score komt even vaak voor.
Spreiding kan een dramatische vorm aannemen. In het plaatje hiernaast staat een zogenaamde uniforme verdeling: elke score komt even vaak voor.
Het gemiddelde is 5,5, evenals de mediaan en de modus. Alleen zien we nu aan deze verdeling, dat een eenduidige interpretatie gewoonweg onmogelijk is: er zijn evenveel mensen euforisch als diep ongelukkig, evenveel mensen best wel ongelukkig als best wel gelukkig en ga zo maar door. Alsof de complexiteit van alledag in een grafiek wordt weergegeven. Bij deze grafiek is “het Nederlandse volk is bijna gelukkig” een onzinnige uitspraak, evenals elke andere conclusie over de 5,5 gemiddeld. De spreiding is zo groot, dat we maar beter niets zeggen over ‘het geluk van Nederland’, omdat ‘het geluk van Nederland’ kennelijk niet is te vatten in één uitspraak of getal. Dit lijkt een overdreven voorbeeld, maar zeg nou eerlijk, heeft u de verdeling van de geluksscores ooit gezien? We weten toch alleen maar dat ‘we’ hoog scoren? Een acht of zo? En wat nou als geluk op een schaal van 1 tot 20 is gemeten? En we weten toch ook dat veel, heel veel mensen een beroep moeten doen op de GGZ? Dus hoe zit het nou?
Het zit zo. Omdat we alleen bericht krijgen over het gemiddelde en daar erg aan hangen, en ons verder niet afvragen hoe de verdeling eruit ziet en op welke schaal er is gemeten, hebben we de schijn gecreëerd dat Nederlanders erg gelukkig zijn, dat 100 km/h veiliger is dan 120 km/h, dat we gemiddeld 32 uur per week werken, en al die andere voorbeelden waarbij ‘we’ op een bepaalde manier ‘scoren’. We missen daardoor erg belangrijke informatie die ons op het spoor kan zetten naar het kennen van de werkelijkheid.
Wisten we tenminste de variantie maar, en liever nog, hadden we ooit maar eens een plaatje van de verdeling gezien, dan waren we een stuk wijzer geweest.
Koornstra, M.J. (1998). The Dutch policy for sustainable road safety; Contribution to the Conference of the Advanced Studies Institute Transport, Environment and Traffic Safety `the role of policies and technologies’, 5-9 April 1994, Amsterdam. D-98-7. SWOV, Leidschendam.
SWOV-Factsheet; Risico in het verkeer ,SWOV Leidschendam, juli 2013
[1] Wat het is maakt in het voorbeeld niet uit.


No Comments - be the first.